130 Cheat Sheet
Author
Drew Ulick
Last Updated
6年前
License
Creative Commons CC BY 4.0
Abstract
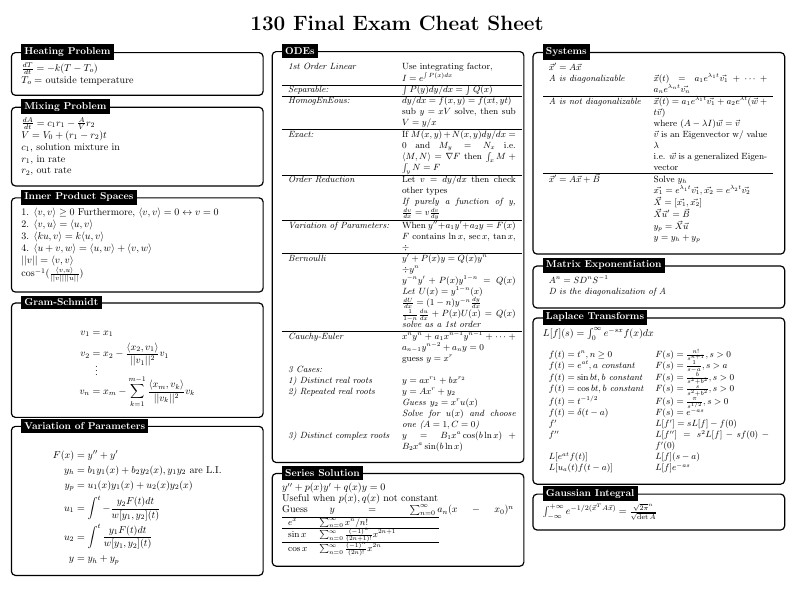
Cheat sheet for Linear Algebra and Differential Equations
Cheat sheet for Linear Algebra and Differential Equations
\documentclass{article}
\usepackage[landscape]{geometry}
\usepackage{url}
\usepackage{multicol}
\usepackage{amsmath}
\usepackage{esint}
\usepackage{amsfonts}
\usepackage{tikz}
\usetikzlibrary{decorations.pathmorphing}
\usepackage{amsmath,amssymb}
\usepackage{colortbl}
\usepackage{xcolor}
\usepackage{mathtools}
\usepackage{amsmath,amssymb}
\usepackage{enumitem}
\makeatletter
\newcommand*\bigcdot{\mathpalette\bigcdot@{.5}}
\newcommand*\bigcdot@[2]{\mathbin{\vcenter{\hbox{\scalebox{#2}{$\m@th#1\bullet$}}}}}
\makeatother
\title{130 Cheat Sheet}
\usepackage[brazilian]{babel}
\usepackage[utf8]{inputenc}
\advance\topmargin-.8in
\advance\textheight3in
\advance\textwidth3in
\advance\oddsidemargin-1.5in
\advance\evensidemargin-1.5in
\parindent0pt
\parskip2pt
\newcommand{\hr}{\centerline{\rule{3.5in}{1pt}}}
%\colorbox[HTML]{e4e4e4}{\makebox[\textwidth-2\fboxsep][l]{texto}
\begin{document}
\begin{center}{\huge{\textbf{130 Final Exam Cheat Sheet}}}\\
\end{center}
\begin{multicols*}{3}
\tikzstyle{mybox} = [draw=black, fill=white, very thick,
rectangle, rounded corners, inner sep=10pt, inner ysep=10pt]
\tikzstyle{fancytitle} =[fill=black, text=white, font=\bfseries]
%------------ Heating ---------------
\begin{tikzpicture}
\node [mybox] (box){%
\begin{minipage}{0.3\textwidth}
$\frac{dT}{dt} = -k(T-T_o)$ \\
$ T_o =$ outside temperature
\end{minipage}
};
%------------ Heating Header ---------------------
\node[fancytitle, right=10pt] at (box.north west) {Heating Problem};
\end{tikzpicture}
%------------ Mixing ---------------
\begin{tikzpicture}
\node [mybox] (box){%
\begin{minipage}{0.3\textwidth}
$\frac{dA}{dt} = c_1r_1-\frac{A}{V}r_2$\\
$V=V_0 +(r_1 - r_2)t$ \\
$c_1$, solution mixture in \\
$r_1$, in rate \\
$r_2$, out rate
\end{minipage}
};
%------------ Mixing Header ---------------------
\node[fancytitle, right=10pt] at (box.north west) {Mixing Problem};
\end{tikzpicture}
%------------ Inner Product Spaces ---------------
\begin{tikzpicture}
\node [mybox] (box){%
\begin{minipage}{0.3\textwidth}
1. $ \langle v,v \rangle \geq 0$ Furthermore, $ \langle v,v \rangle = 0 \leftrightarrow v = 0 $ \\
2. $\langle v,u \rangle = \langle u,v \rangle $ \\
3. $ \langle ku,v \rangle =k\langle u,v \rangle $ \\
4. $\langle u+v,w\rangle = \langle u,w \rangle + \langle v,w\rangle $ \\
$ ||v|| = \langle v, v \rangle $ \\
$ \cos^{-1}(\frac{\langle v,u \rangle}{||v|| ||u||}) $
\end{minipage}
};
%------------ Inner Product Space Header ---------------------
\node[fancytitle, right=10pt] at (box.north west) {Inner Product Spaces};
\end{tikzpicture}
%------------ Gram-Schmidt Content ---------------
\begin{tikzpicture}
\node [mybox] (box){%
\begin{minipage}{0.3\textwidth}
\begin{align*}
v_{1} &= x_{1} \\
v_{2} &= x_{2} - \frac{\langle x_2, v_1\rangle}{||v_{1}||^2}v_{1}\\
&\shortvdotswithin{=}
v_{n} &= x_{m} - \sum_{k=1}^{m-1} \frac{\langle x_{m},v_{k} \rangle}{||v_{k}||^{2}}v_{k}
\end{align*}
\end{minipage}
};
%------------ Gram-Schmidt Header ---------------------
\node[fancytitle, right=10pt] at (box.north west) {Gram-Schmidt};
\end{tikzpicture}
%------------ Variation of Parameters Content ---------------------
\begin{tikzpicture}
\node [mybox] (box){%
\begin{minipage}{0.3\textwidth}
\begin{align*}
F(x) &= y'' + y' \\
y_h &= b_1y_1(x) + b_2y_2(x), y_1 y_2 \text{ are L.I.} \\
y_p &= u_1(x)y_1(x) + u_2(x)y_2(x) \\
u_1 &= \int^t -\frac{y_2F(t)dt}{w[y_1,y_2](t)} \\
u_2 &= \int^t \frac{y_1F(t)dt}{w[y_1,y_2](t)} \\
y &= y_h + y_p
\end{align*}
\end{minipage}
};
%------------ Variation of Parameters Header ---------------------
\node[fancytitle, right=10pt] at (box.north west) {Variation of Parameters};
\end{tikzpicture}
%------------ ODE Content ---------------
\begin{tikzpicture}
\node [mybox] (box){%
\begin{minipage}{0.3\textwidth}
\small{
\begin{tabular}{lp{4cm} l}
\textit{1st Order Linear} & Use integrating factor,
\\ & $I = e^{\int P(x) dx}$ \\ \hline
\textit{Separable:} & $ \int P(y) dy/dx = \int Q(x) $ \\ \hline
\textit{HomogEnEous:} & $ dy/dx = f(x,y) = f(xt,yt) $ \\ &
sub $ y = xV $ solve, then sub $ V = y/x $ \\ \hline
\textit{Exact:} & If $ M(x,y) + N(x,y)dy/dx = 0 $ and $ M_y = N_x $ i.e. $ \langle M,N \rangle = \nabla F $ then $ \int_x M + \int_y N = F $ \\ \hline
\textit{Order Reduction} & Let $ v = dy/dx $ then check other types \\
&\textit{If purely a function of y, }$\frac{dv}{dx} = v\frac{dv}{dy}$\\
\hline
\textit{Variation of Parameters:} & When $y''+a_1y'+a_2y = F(x)$ \\
& $F$ contains $\ln x$, $\sec x$, $\tan x$, $\div$ \\ \hline
\textit{Bernoulli} & $y' + P(x)y = Q(x)y^n$ \\
& $\div y^n$ \\
&$y^{-n}y'+P(x)y^{1-n}=Q(x)$ \textit{Let }$U(x) = y^{1-n}(x)$ \\
&$\frac{dU}{dx}=(1-n)y^{-n}\frac{dy}{dx}$ \\
&$\frac{1}{1-n}\frac{du}{dx} + P(x)U(x) = Q(x)$ \textit{solve as a 1st order} \\ \hline
\textit{Cauchy-Euler} &$x^ny^n + a_1x^{n-1}y^{n-1} + \cdots + a_{n-1}y^{n-2}+a_ny = 0$ \\
&guess $y = x^r$ \\
\textit{3 Cases:} \\
\textit{1) Distinct real roots} &$y = ax^{r_1}+bx^{r_2}$ \\
\textit{2) Repeated real roots} &$y = Ax^r + y_2$ \\
&\textit{Guess} $y_2 = x^ru(x)$ \\
&\textit{Solve for $u(x)$ and choose one ($A=1, C=0$)} \\
\textit{3) Distinct complex roots} &$y=B_1x^a \cos (b \ln x) + B_2x^a\sin (b \ln x)$
\end{tabular}}
\end{minipage}
};
%------------ ODE Header ---------------------
\node[fancytitle, right=10pt] at (box.north west) {ODEs};
\end{tikzpicture}
%------------ Series Solution Content ---------------
\begin{tikzpicture}
\node [mybox] (box){%
\begin{minipage}{0.3\textwidth}
$y'' + p(x)y' + q(x)y = 0$ \\
Useful when $p(x), q(x)$ not constant \\
Guess $y = \sum_{n=0}^{\infty}a_n(x-x_0)^n$
\small{
\begin{tabular}{lp{4cm} l}
\hline
$e^x$ & $\sum_{n=0}^{\infty} x^n/{n!}$ \\ \hline
$\sin x$ & $\sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)!}x^{2n+1}$ \\ \hline
$\cos x$ & $\sum_{n=0}^{\infty} \frac{(-1)^n}{(2n)!}x^{2n}$ \\
\end{tabular}}
\end{minipage}
};
%------------ Series Solution Header ---------------------
\node[fancytitle, right=10pt] at (box.north west) {Series Solution};
\end{tikzpicture}
%------------ Systems of ODE Content ---------------
\begin{tikzpicture}
\node [mybox] (box){%
\begin{minipage}{0.3\textwidth}
\small{
\begin{tabular}{lp{4cm} l}
$\vec{x}' = A\vec{x}$ \\
\textit{A is diagonalizable} & $\vec{x}(t)=a_{1}e^{\lambda_1 t}\vec{v_1}+\cdots+ a_{n}e^{\lambda_n t}\vec{v_n}$ \\ \hline
\textit{A is not diagonalizable} & $\vec{x}(t)=a_1e^{\lambda_1 t}\vec{v_1} + a_2e^{\lambda t}(\vec{w} + t\vec{v} )$ \\
& where $(A - \lambda I)\vec{w} = \vec{v} $\\
& $\vec{v}$ is an Eigenvector w/ value $\lambda$ \\
& i.e. $\vec{w}$ is a generalized Eigenvector \\ \hline
$\vec{x}' = A\vec{x} + \vec{B}$ &Solve $y_h$ \\
& $\vec{x_1} = e^{\lambda_1t}\vec{v_1}, \vec{x_2} = e^{\lambda_2t}\vec{v_2}$ \\ & $\vec{X} = [\vec{x_1},\vec{x_2}]$ \\
& $\vec{X}\vec{u}'=\vec{B}$ \\
& $y_p = \vec{X}\vec{u}$ \\
& $y = y_h + y_p$
\end{tabular}}
\end{minipage}
};
%------------ Systems of ODE Header ---------------------
\node[fancytitle, right=10pt] at (box.north west) {Systems};
\end{tikzpicture}
%------------ Exponentiation Content ---------------
\begin{tikzpicture}
\node [mybox] (box){%
\begin{minipage}{0.3\textwidth}
\small{
\begin{tabular}{lp{4cm} l}
$A^n = SD^nS^{-1}$ \\
\textit{D is the diagonalization of A}
\end{tabular}}
\end{minipage}
};
%------------ Spring-Mass Header ---------------------
\node[fancytitle, right=10pt] at (box.north west) {Matrix Exponentiation};
\end{tikzpicture}
\
%------------ Laplace Transforms Content ---------------
\begin{tikzpicture}
\node [mybox] (box){%
\begin{minipage}{0.3\textwidth}
$L[f](s) = \int_0^{\infty} e^{-sx}f(x)dx $\\
\small{
\begin{tabular}{lp{4cm} l}
$f(t) = t^n, n \geq 0 $ &$F(s) = \frac{n!}{s^{n+1}}, s > 0 $ \\
$f(t) = e^{at}, a \textit{ constant}$ & $ F(s) = \frac{1}{s-a}, s > a$ \\
$f(t) = \sin{bt}, b \textit{ constant}$ & $ F(s) = \frac{b}{s^2 + b^2}, s > 0$ \\
$f(t) = \cos{bt}, b \textit{ constant}$ & $ F(s) = \frac{s}{s^2 + b^2}, s > 0$ \\
$f(t) = t^{-1/2}$ & $F(s) = \frac{\pi}{s^{1/2}}, s > 0$ \\
$f(t) = \delta(t-a)$ & $F(s) = e^{-as}$ \\
$f'$ & $L[f'] = sL[f] - f(0)$ \\
$f''$ & $L[f''] = s^2 L[f] - sf(0) - f'(0)$ \\
$L[e^{at}f(t)]$ & $L[f](s-a)$ \\
$L[u_a(t)f(t-a)]$ & $L[f]e^{-as}$
\end{tabular}}
\end{minipage}
};
%------------ Laplace Transforms Header ---------------------
\node[fancytitle, right=10pt] at (box.north west) {Laplace Transforms};
\end{tikzpicture}
%------------ Gaussian Integral Content ---------------------
\begin{tikzpicture}
\node [mybox] (box){%
\begin{minipage}{0.3\textwidth}
$\int_{-\infty}^{+\infty} e^{-1/2(\vec{x}^TA\vec{x})} = \frac{\sqrt{2\pi}^n}{\sqrt{\det A}}$
\end{minipage}
};
%------------ Gaussian Integral Header ---------------------
\node[fancytitle, right=10pt] at (box.north west) {Gaussian Integral};
\end{tikzpicture}
\\
\\
\\
\\
%------------ Complex Numbers Content ---------------------
\begin{tikzpicture}
\node [mybox] (box){%
\begin{minipage}{0.3\textwidth}
\small{
\begin{tabular}{lp{4cm} l}
\textit{Systems of equations} & If $\vec{w_1} = \vec{u(t)} + i\vec{v(t)}$ is a solution, $\vec{x_1} = \vec{u(t)}, \vec{x_2} = \vec{v(t)}$ are solutions \\
& i.e. $\vec{x_h} = c_1 \vec{x_1} + c_2 \vec{x_2}$ \\
\hline
\textit{Euler's Identity} &$e^{ix} = \cos x + i \sin x$
\end{tabular}
}
\end{minipage}
};
%------------ Gaussian Integral Header ---------------------
\node[fancytitle, right=10pt] at (box.north west) {Complex Numbers};
\end{tikzpicture}
%------------ Vector Spaces ---------------
\begin{tikzpicture}
\node [mybox] (box){%
\begin{minipage}{0.3\textwidth}
$v_1, v_2 \in V$\\
1. $v_1 + v_2 \in V$ \\
2. $k \in \mathbb{F}, kv_1 \in V $ \\
3. $ v_1 + v_2 = v_2 + v_1 $ \\
4. $(v_1 + v_2) + v_3 = v_1 + (v_2 + v_3) $ \\
5. $\forall v \in V, 0 \in V \mid 0 + v_1 = v_1 + 0 = v_1$ \\
6. $\forall v \in V, \exists -v \in V \mid v + (-v) = (-v) + v = 0 $ \\
7. $\forall v \in V, 1 \in \mathbb{F} \mid 1*v = v$ \\
8. $\forall v \in V, k,l \in \mathbb{F}, (kl)v = k (lv)$ \\
9. $\forall k \in \mathbb{F}, k(v_1 + v_2) = kv_1 + kv_2$ \\
10. $\forall v \in V, k,l \in \mathbb{F}, (k+l)v = kv + lv$
\end{minipage}
};
%------------ Vector Space Header ---------------------
\node[fancytitle, right=10pt] at (box.north west) {Vector Spaces};
\end{tikzpicture}
\end{multicols*}
\end{document}
Contact GitHub API Training Shop Blog About
© 2016 GitHub, Inc. Terms Privacy Security Status Help